
No definition was really thought necessary, and in fact the mathematics was considered the science of magnitudes. Real numbers became very much associated with magnitudes.
#Real numbers series
This leads into the study of infinite series but without the necessary machinery to prove that these infinite series converged to a limit, he was never going to be able to progress much further in studying real numbers. He considered approximations by continued fractions, and also approximations by taking successive square roots.

For Wallis there were a variety of ways that one might achieve this approximation, so coming as close as one pleased. Now, as for other incommensurable quantities, though this proportion cannot be accurately expressed in absolute numbers, yet by continued approximation it may so as to approach nearer to it than any difference assignable. such proportion is not to be expressed in the commonly received ways of notation: particularly that for the circles quadrature. However, Wallis understood that there were proportions which did not fall within this definition of number, such as those associated with the area and circumference of a circle:. He still only considers finite decimal expansions and realises that with these one can approximate numbers (which for him are constructed from positive integers by addition, subtraction, multiplication, division and taking nth roots ) as closely as one wishes. Details of the earlier contributions are examined in some detail in our article: The real numbers: Pythagoras to Stevin If we move forward almost exactly 100 years to the publication of A treatise of Algebra by Wallis in 1684 we find that he accepts, without any great enthusiasm, the use of Stevin's decimals. The values that make the equation true, the solutions, are found using the properties of real numbers and other results.By the time Stevin proposed the use of decimal fractions in 1585, the concept of a number had developed little from that of Euclid's Elements. The equation is not inherently true or false, but only a proposition.
The expressions can be numerical or algebraic.
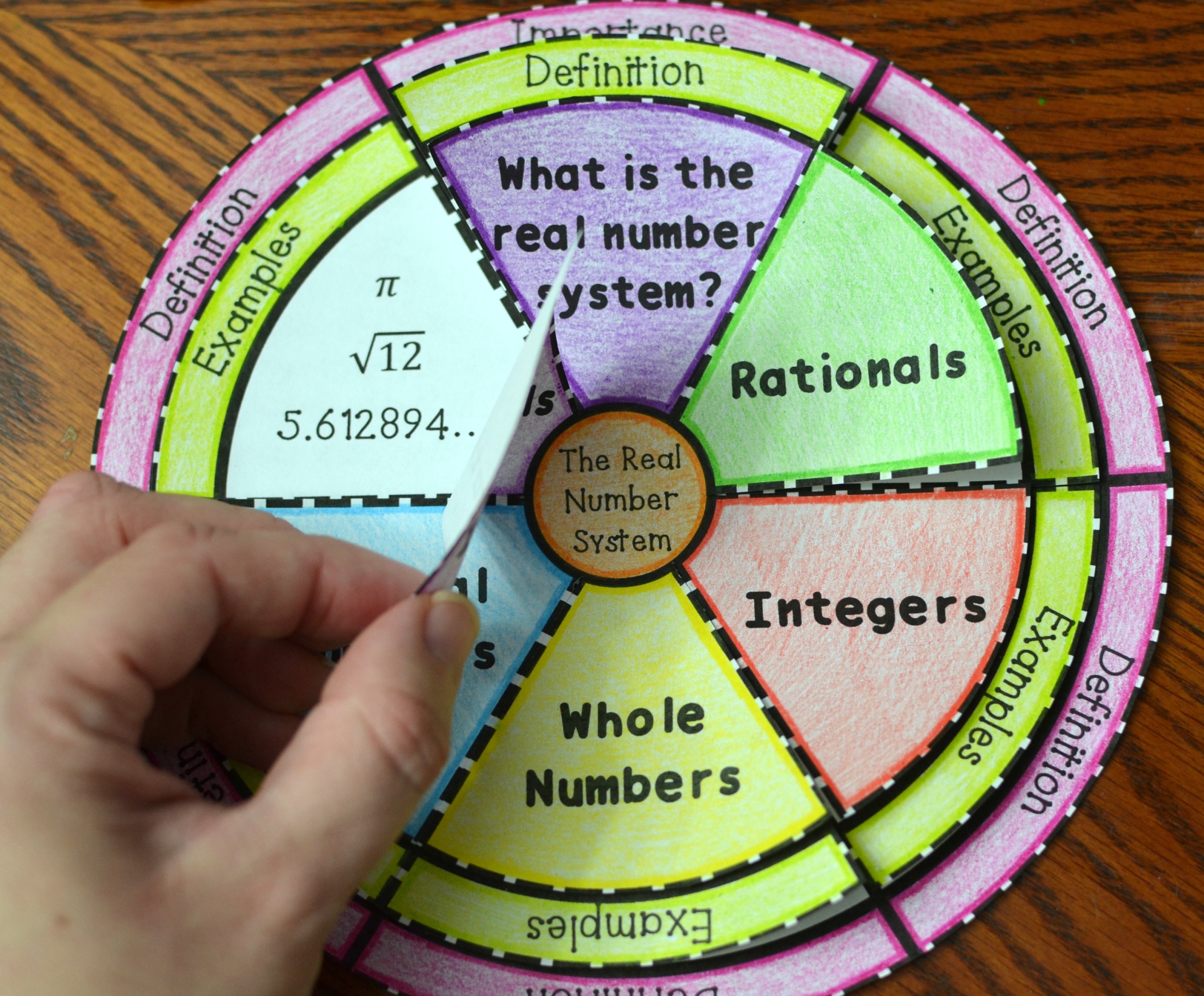
#Real numbers how to
In the following video we present more examples of how to evaluate an expression for a given value.Īn equation is a mathematical statement indicating that two expressions are equal. If the algebraic expression contains more than one variable, replace each variable with its assigned value and simplify the expression as before. Replace each variable in the expression with the given value, then simplify the resulting expression using the order of operations. To evaluate an algebraic expression means to determine the value of the expression for a given value of each variable in the expression. When that happens, the value of the algebraic expression changes. In each case, the exponent tells us how many factors of the base to use, whether the base consists of constants or variables.Īny variable in an algebraic expression may take on or be assigned different values. The numbers we use for counting, or enumerating items, are the natural numbers: 1, 2, 3, 4, 5, and so on. In this section we will explore sets of numbers, perform calculations with different kinds of numbers, and begin to learn about the use of numbers in algebraic expressions.

Evaluate and simplify algebraic expressions.īecause of the evolution of the number system, we can now perform complex calculations using several categories of real numbers.



 0 kommentar(er)
0 kommentar(er)
